Logic will get you from A to B. Imagination will take you everywhere.
—Albert Einstein
Logisch datamodel
In dit hoofdstuk introduceren we het concept ‘databankmodel’ als inleiding om het logische datamodel op te bouwen. Van daaruit kunnen we dan de omzetting van het conceptueel naar het logisch datamodel overlopen. We bekijken:
- Wat is een databankmodel?
- Wat is de rol van een databankmodel?
- Wat is het relationeel databankmodel?
- Hoe zet je een conceptueel datamodel om naar een logisch datamodel volgens het relationeel databankmodel?
Jullie moeten de volgende termen kunnen uitleggen, hoe we dit weergeven (waar relevant) en toelichten aan de hand van een voorbeeld:
- logisch datamodel;
- databankmodel;
- relationeel databankmodel;
- tabel;
- sleutel (waaronder kandidaatsleutel, primaire sleutel, vreemde sleutel, samengestelde sleutel, natuurlijke sleutel, technische of surrogaatsleutel)
- normaliseren.
Op het einde van dit hoofdstuk moet je de notatie van een logisch datamodel (van een relationeel databankmodel) kennen en kunnen toelichten aan de hand van een voorbeeld.
Je moet daarnaast ook in staat zijn om een conceptueel datamodel om te zetten naar een logisch datamodel (van een relationeel databankmodel).
Inleiding
Na het conceptueel datamodel gaan we verder met het ontwerp van onze databank. We hadden een databank omschreven als een verzameling van ‘persistente data’. Om te bepalen wat er specifiek in die verzameling opgenomen moet worden, hebben we het conceptueel datamodel opgesteld die de vraag ‘Welke informatie moeten we in onze databank opnemen‘ beantwoordt. Daarbij wordt de verzameling afgebakend tot een bepaald thema of toepassing. Een voorbeeld hiervan is de databank van de UCLL Hogeschool studentenadministratie, met data betreffende studenten, opleidingen, inschrijvingen, ...
In een volgende stap gaan we nadenken over de structuur van deze verzameling van data. Hoe organiseren we de data? Dat kan immers op verschillende manieren.
Vooraleer we verder focussen op de verschillende manieren hoe we structuur kunnen toepassen, moeten we even stilstaan bij de vraag ‘Waarom is structuur belangrijk?’. Wanneer we met machines werken, zorgt structuur ervoor dat we deze computers kunnen aanleren om binnen het kader van deze structuur te werken. De structuur op zich zorgt voor voorspelbaarheid zodat het makkelijk wordt om hier procedures op te definiëren. Dit geldt trouwens niet alleen voor computers, het feit dat er markeringen zijn op de wegen structureert de wegen op zo‘n manier dat er regels kunnen worden bepaald die de verkeersveiligheid bevorderen. En daar zijn we allemaal blij om.
Voor data geeft dit dan nog eens het bijkomende voordeel dat structuur op zich bijkomende informatie bevat (we noemen dit metadata - data over de data) die dan gebruikt kan worden voor het bepalen van procedures. Zodoende kunnen we de toegang tot de data beheren, opslag optimaliseren, standaardprocedures ontwikkelen, ...
Je kan eenzelfde concept op heel wat verschillende manieren structureren, denk maar aan een bibliotheek. Je kan alle boeken rangschikken volgens thema, volgens auteur, volgens titel, ... Voor data is dit niet anders. Je stelt dan de volgende vragen:
- over welk type van data spreken we?
- wat wil je met deze data gaan doen?
Omdat IT'ers nogal houden van standaarden (en jullie als toekomstige IT'ers ondertussen enthousiast moeten worden omdat er duidelijk een standaard aan zit te komen), zou het geen verrassing mogen zijn dat dit ook voor data het geval is. Er zijn doorheen de tijd al heel wat standaarden bepaald voor datamodellen en om data te structureren. We noemen deze standaarden databankmodellen.
Databankmodellen
Een databankmodel bepaalt de structuur van een databank en hoe de data binnen een databank wordt georganiseerd en gemanipuleerd. Laten we dit even verder uitdiepen.
Eerst en vooral zal een databankmodel data op een specifieke manier gaan structureren. Daarbij wordt typisch gebruik gemaakt van een aantal componenten of bouwblokken die elk een rol spelen in de structuur van het datamodel. Die rol wordt dan typisch beschreven in een aantal principes of regels die de samenwerking van de verschillende componenten vastlegt.
De standaarden rond databankmodellen (en andere domeinen) geven nog een aantal belangrijke voordelen die we zeker niet uit het oog mogen verliezen:
- Eerst en vooral gaat het om standaarden die over heel de industrie gebruikt worden . Wanneer jullie het in jullie professionele loopbaan over een bepaalde standaard hebben, begrijpt iedereen rond de tafel met een IT-opleiding waarover je het hebt. Dit geldt ook voor databankmodellen.
- Een tweede voordeel is dat heel wat onderzoekers blijven verder werken op deze standaarden en bijkomende uitbreidingen (herinner EERD). Ze blijven procedures ontwikkelen waar iedereen baat bij heeft, dus standaarden blijven typisch wel evolueren. Het is jullie taak om bij te blijven. Levenslang leren …
- Een derde voordeel is dat de standaarden een basis vormen voor bedrijven om softwareproducten te ontwikkelen . Aangezien ze gebaseerd zijn op standaarden kunnen ze op hun beurt goed samenwerken met andere producten die dan ook weer standaarden gebruiken.
Over de jaren heen zijn er heel wat verschillende databankmodellen ontwikkeld. Sommige zijn ontwikkeld vanuit bepaalde technologieën. Anderen om met nieuwe types van data te kunnen werken. Anderen dan weer omdat de ontwikkeling van al maar krachtigere machines de mogelijkheden om met data te werken hebben uitgebreid. Kortom de horizon van het mogelijke breidt constant uit, en zo ook het aanbod aan beschikbare databankmodellen.
Van al deze databankmodellen gaat er één specifiek databankmodel al een hele tijd mee. Het relationeel databankmodel, in de jaren 70 door Codd ontwikkeld, geldt vandaag nog steeds als een standaard binnen de IT-industrie. Binnen dit vak is dit dan ook het databankmodel waarop we verder de focus leggen. Enkele andere komen in andere vakken aan bod.
Relationeel databankmodel
Tabel
Het relationeel databankmodel maakt gebruik van één component of bouwblok, de tabel. Alle data die we willen bijhouden, zullen we in één of meerdere tabellen gieten. Elke tabel stelt een verzameling gelijkaardige data voor, bijvoorbeeld een tabel met alle gegevens van studenten. Een tabel is gestructureerd als een 2-dimensionale matrixstructuur, waarbij we de horizontale dimensie de rijen noemen en de verticale dimensie de kolommen.
Een rij stelt een record (of entiteit) voor van de tabel. Een tabel kan theoretisch een oneindig aantal rijen bevatten. Als we een tabel creëren met studentengegevens, zou elke rij een student kunnen voorstellen.
Een kolom stelt een attribuut (of eigenschap) van de tabel voor die telkens een stukje beschrijving van de rij (of entiteit) zal bevatten. Een tabel bevat een vast aantal kolommen. Indien we een kolom willen toevoegen, wat op zich wel mogelijk is, moeten we nadenken wat dit voor de bestaande rijen in de tabel betekent. Zo is het mogelijk dat we een waarde voor deze kolom moeten invullen voor elk van de rijen die in de tabel al opgenomen zijn.
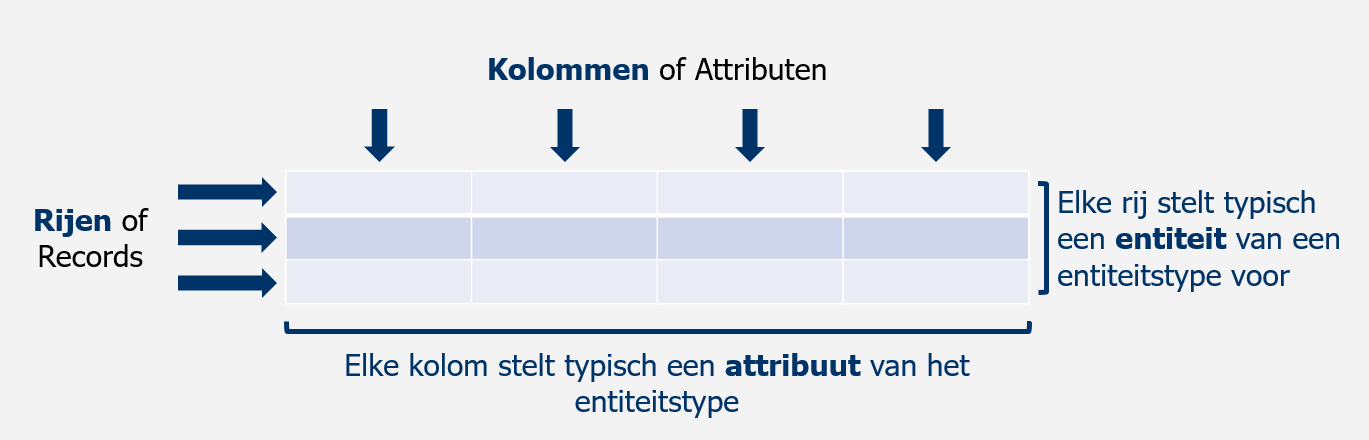
In ons voorbeeld van een tabel met studentengegevens, zou elke kolom een bepaalde eigenschap van de student bevatten, bijvoorbeeld de naam, de geboortedatum, ...
Omdat een tabel een specifieke structuur heeft van kolommen, zal dus ook alle data die in één tabel wordt bijgehouden, altijd dezelfde structuur hebben. Telkens we bijkomende data met een andere structuur bijhouden, creëren we een bijkomende tabel. In een relationeel databankmodel noemen we het geheel van een aantal tabellen ‘een databank’. Onze relationele databank kan dus heel wat verschillende tabellen bevatten. Om deze tabellen dan vervolgens met elkaar te combineren en verbanden te creëren, maken we gebruik van sleutels.
Sleutels
Een sleutel bestaat uit één of meerdere kolommen (attributen) van een tabel die voldoet aan de volgende drie voorwaarden:
- De waarde van de combinatie van één of meerdere kolommen in een rij vormt een unieke identificatie van de volledige rij. Voor elke rij moet de waarde van de sleutel dus uniek zijn, anders gezegd mogen twee rijen in de tabel niet eenzelfde sleutel hebben.
- De combinatie van de kolommen die de sleutel vormen moet minimaal zijn. Daarmee willen we aangegeven dat indien we in de combinatie één van de kolommen zouden verwijderen, we niet meer zouden voldoen aan de eerste voorwaarde. Indien we een sleutel hebben die bestaat uit één kolom, is onze sleutel per definitie minimaal.
- De waarde van de sleutel mag ook niet leeg zijn, de sleutel moet dus altijd ingevuld zijn.
Binnen het relationeel model bepalen we voor elke tabel één primaire sleutel (primary key). De waarde van de primaire sleutel vormt voor elke rij een unieke identificatie. Deze primaire sleutel gebruiken we om de verschillende tabellen met elkaar te verbinden.
De primaire sleutel wordt gekozen uit een aantal kandidaatsleutels. Een kandidaatsleutel (candidate key) is een potentiële sleutel voor een tabel, die dus ook voldoet aan de drie voorwaarden waaraan een sleutel moet voldoen.
Onderstaande afbeelding geeft een voorbeeld voor de tabel ‘Lectoren’. We hebben vier kolommen die mogelijk een sleutel aanbieden. Na overweging houden we enkel ‘Lector ID’ over als kandidaatsleutel. Aangezien er maar één kandidaatsleutel is, is de keuze logisch om dit als de primaire sleutel te gaan gebruiken.
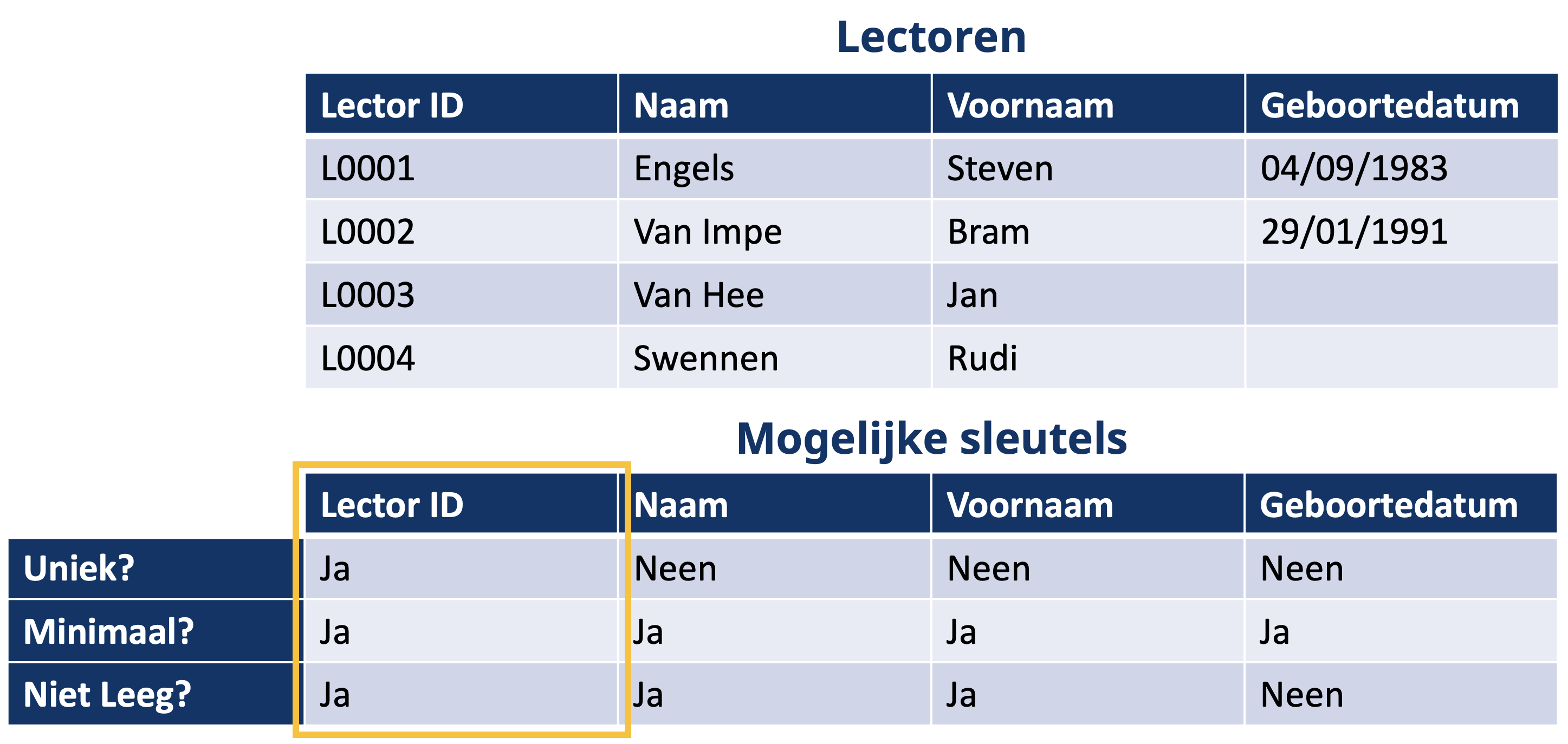
Een tabel kan dus meerdere sleutels hebben. Vanuit de lijst van kandidaatsleutels kiezen we één primaire sleutel. Om een goede sleutel te kiezen vanuit de lijst van mogelijke sleutels kan je de volgende criteria in rekening nemen:
- Een sleutel moet zo stabiel mogelijk zijn. We gaan er zelfs vanuit dat een sleutel eigenlijk nooit aangepast wordt. Hier zijn enkele uitzonderingen op, maar we proberen een veranderende primaire sleutel hoe dan ook te vermijden. Bijvoorbeeld, indien je binnen de context van studentenadministratie de keuze hebt tussen een rijksregisternummer of een studentennummer om een student uniek te identificeren, kies je een studentennummer. Niet enkel hebben we binnen de studentenadministratie meer controle over het studentennummer, we kunnen er over waken dat dit nooit aangepast wordt. Een rijksregisternummer kan wel veranderen. Daarbij is het gebruik van een rijksregisternummer in een databank (en erbuiten) onderhevig aan heel strikte GDPR wetgeving, maar dat leggen we in een ander vak uit.
- Een sleutel omvat ideaal zo weinig mogelijk kolommen. Sleutels kunnen uit één of meerdere kolommen bestaan. Een sleutel die bestaat uit meerdere kolommen, noemen we een samengestelde sleutel simpelweg omdat dit samengesteld wordt uit meerdere waarden. We vermijden samengestelde sleutels omdat dat het geheel wat complexer maakt, en complexiteit brengt een kost met zich mee die we trachten te vermijden. Complexiteit betekent dat het geheel moeilijk te begrijpen is voor de betrokken partijen, mogelijk een verlies aan performantie bij het verwerken van de data, enz. Van zodra jullie in andere vakken bijleren rond performantie, automatisatie, security, … zullen we meer in staat zijn om de kost van complexiteit in een databank toe te lichten.
- Een sleutel is idealiter een eenvoudige waarde, bijvoorbeeld een nummer of een korte opeenvolging van karakters. Van zodra het complexer wordt, of zelfs speciale karakters gaat gebruiken, wordt het risico op fouten groter.
- Een sleutel wordt idealiter genomen uit de context van datgene wat we beschrijven. Een sleutel die zowel waardevol is binnen de databank (als primaire sleutel) maar ook buiten het systeem gebruikt wordt, heeft als voordeel dat heel wat betrokken personen snel begrijpen waarover het gaat. Bijvoorbeeld, een studentennummer is ook buiten de databank een manier om studenten te identificeren. Dus is dat studentennummer mogelijk een goede primaire sleutel. Een sleutel die zowel gebruikt wordt binnen de databank als erbuiten, noemen we een natuurlijke sleutel (natural key).
Indien we geen kandidaatsleutels hebben, of de beschikbare kandidaatsleutels zijn geen geschikte keuze, hebben we altijd de mogelijkheid om zelf een sleutel te definiëren. We noemen die een technische sleutel of surrogaatsleutel. De technische sleutel wordt enkel binnen de databank gebruikt, en heeft buiten de databank geen waarde. Het heeft dan als effect dat we een bijkomende kolom bijmaken die de sleutel zal bevatten.
Uiteindelijk moet elke tabel een primaire sleutel hebben. We hadden al aangegeven dat de primaire sleutels het mogelijk maken om verbanden te creëren tussen de tabellen. Dit gebeurt door een uitwisseling van primaire sleutels. Het mechanisme van de uitwisseling wordt toegelicht in het deel ‘Van conceptueel naar logisch datamodel‘. Het komt erop neer dat de primaire sleutel van de ene tabel toegevoegd wordt aan een andere tabel. Van zodra we een primaire sleutel toevoegen aan een andere tabel, en dus een kolom toevoegen aan die tabel, noemen we deze sleutel een vreemde sleutel (foreign key).
Het gebruik van de primaire sleutels en vreemde sleutels staat centraal in het relationeel model. Het is de basis om de relaties vast te leggen en te definiëren.
Andere databankmodellen
Naast het relationele databankmodel, zijn er ook heel wat andere databankmodellen, elk met hun specifieke toepassing. Bepaalde van deze databankmodellen hebben hun weg gevonden in bepaalde technologieën zodat een goed begrip van de modellen jullie in staat moet stellen om de werking van de technologie te begrijpen. We gaan hier in andere vakken dieper op in, maar om jullie alvast een voorsmaakje te geven, hebben we alvast enkele databankmodellen opgelijst:
- Hiërarchisch databankmodel: maakt gebruik van boom-structureren om data voor te stellen
- Netwerk databankmodel: maakt gebruik van netwerk-structureren om data voor te stellen
- Dimensionaal databankmodel: gebruikt in de context van data warehouses
- Object-georiënteerd databankmodel: combineert de mogelijkheden van een relationeel databankmodel met het object-georiënteerd programmeren
- Graaf databankmodel: maakt gebruik van graaf-structureren om data voor te stellen
Van conceptueel naar logisch datamodel
Hoe je een logisch datamodel tekent in draw.io vind je in een apart hoofdstuk in twee video's:
Het logisch datamodel beantwoordt de vraag ‘Hoe moeten we de data structureren volgens ons gekozen databankmodel?’. We hebben een conceptueel datamodel ontwikkeld, en de keuze gemaakt voor een relationeel databankmodel. De omzetting van dit conceptueel datamodel verloopt vervolgens in een aantal stappen.
Stap 1: entiteittypes worden tabellen
In de eerste stap creëren we een tabel voor elk van de entiteittypes. Deze tabel geven we dezelfde naam als het entiteittype. Vervolgens definiëren we de kolommen van de tabel, waarbij we voor elk attribuut een kolom aanmaken , met uitzondering van de meerwaardige attributen en de afgeleide attributen. We komen later nog terug op de meerwaardige attributen. De naam van de gecreëerde kolom komt overeen met de naam van het attribuut.
De notatie van het logisch datamodel is verschillend van dat van het conceptueel datamodel. We geven het geheel van een tabel weer als een kader, met hierin een lijst van de attributen.
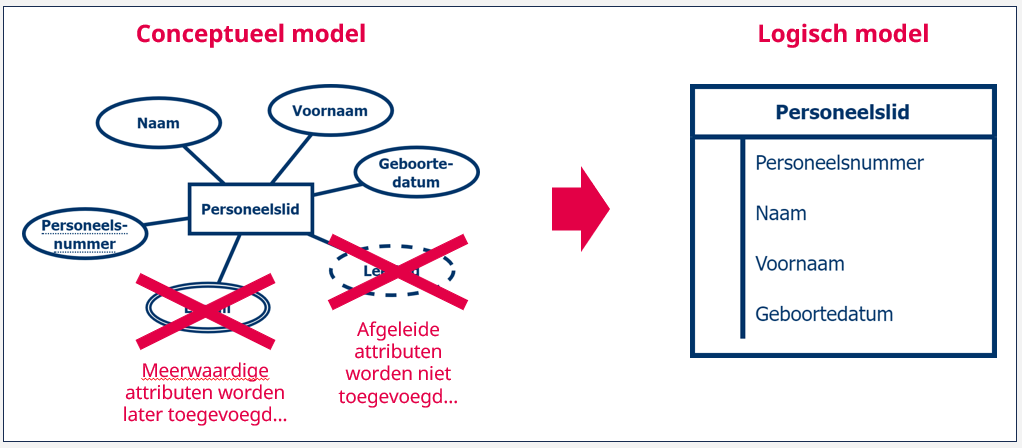
Stap 2: elke tabel krijgt een primaire sleutel toegewezen
In een tweede stap duiden we voor elke tabel een primaire sleutel aan. Dat betekent dat we een aantal kandidaatsleutels moeten bepalen en vanuit deze lijst vervolgens de beste kandidaat selecteren.
We duiden de primaire sleutel aan door de kolommen van de sleutel bovenaan de lijst te plaatsen met hieronder een lijn om duidelijk een onderscheid te maken tussen de primaire sleutel en de resterende kolommen. Daarbij zetten we ook voor de verschillende kolommen van de primaire sleutel de code ‘PK’ (van primary key) en om volledig zeker te zijn dat niemand zich kan vergissen, onderlijnen we de kolomnamen ook nog eens.
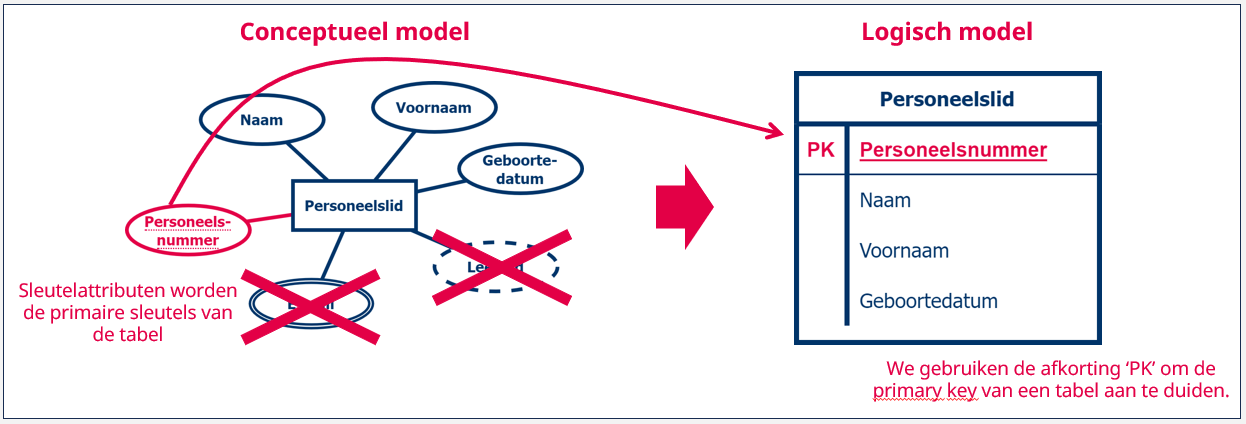
We doen dit voor elke tabel. Houd ook in het achterhoofd dat je een technische sleutel mag aanmaken, als het moeilijk is om met de bestaande kolommen een primaire sleutel te maken.
Stap 3: voor elke 1-1 en 1-N relaties zetten we de primaire sleutel over als vreemde sleutel
In de derde stap gaan we al enkele van de relaties vanuit het conceptueel datamodel omzetten naar iets equivalents in het logisch datamodel . Aangezien we binnen het logisch datamodel verbanden creëren door middel van sleutels, gaan we dus hiermee aan de slag.
Voor elke 1-N relatie gaan we de primaire sleutel van de 1-zijde overdragen naar de N-zijde. Aan de N-zijde wordt deze primaire sleutel dan een vreemde sleutel. Elke rij van de tabel aan de N-zijde zal dus een bijkomende kolom krijgen met hierin een verwijzing (door middel van de primaire sleutel) naar een rij in de tabel van de 1-zijde.
We hebben bijvoorbeeld twee entiteittypes: ‘Team’ en ‘Personeelslid’. Elk personeelslid zit in exact één team. Elk team kan meerdere personeelsleden omvatten. We creëren twee tabellen: een tabel ‘Team’ en een tabel ‘Personeelslid’. De tabel ‘Team’ krijgt als primaire sleutel ‘Teamcode’, waarbij elk team in de tabel een unieke teamcode krijgt. De tabel ‘Personeelslid’ krijgt als primaire sleutel ‘Personeelsnummer’, waarbij elk personeelslid in de tabel een uniek personeelsnummer krijgt. Om het verband tussen de twee entiteittypes aan te duiden in het logisch datamodel, voegen we de teamcode vanuit de ‘Team‘ tabel (1-zijde) toe aan elk personeelslid in de ‘Personeelslid‘ tabel (N-zijde).
Het omgekeerde (nl. de primaire sleutel van Personeelslid toevoegen aan Team) is geen optie. We kunnen aan een team slechts één waarde toevoegen. Als we dus een verwijzing zouden maken vanuit het team naar één personeelslid, zijn we het verband met de andere teamleden van het team kwijt.
In het datamodel voegen we de vreemde sleutel toe aan de lijst van kolommen . We duiden de vreemde sleutel aan met de afkorting ‘FK’ (van foreign key) gevolgd door een volgnummer, bijvoorbeeld FK1, FK2, ... Het volgnummer moet het mogelijk maken om de verschillende vreemde sleutels van elkaar te onderscheiden. Indien we een vreemde sleutel hebben die uit meerdere kolommen bestaat, zetten we elk van de kolommen over. We geven ze dan allemaal hetzelfde volgnummer om aan te duiden dat ze samen horen.
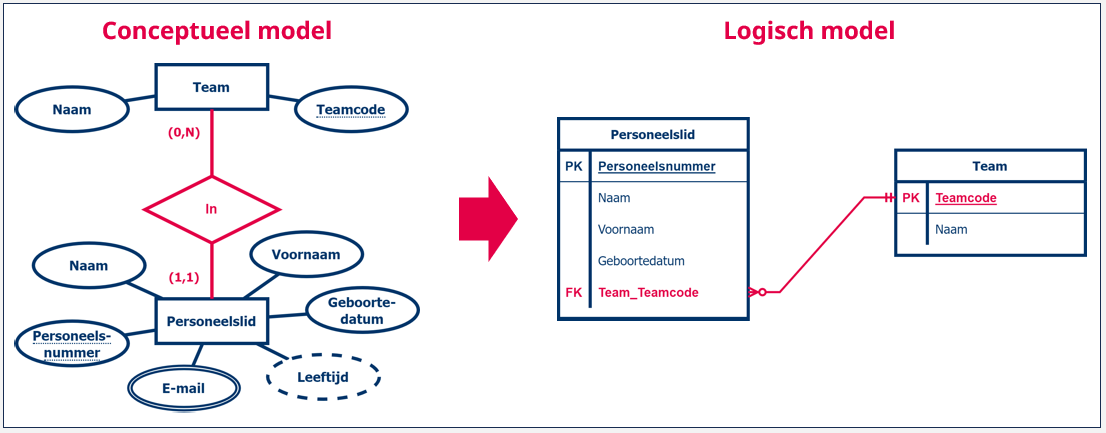
Het verband duiden we nog steeds aan door een lijn waarbij we de kraaienpootnotatie gebruiken. De kraaienpootnotatie is verschillend van de (min,max) notatie die jullie tot nu toe gebruikt hebben.
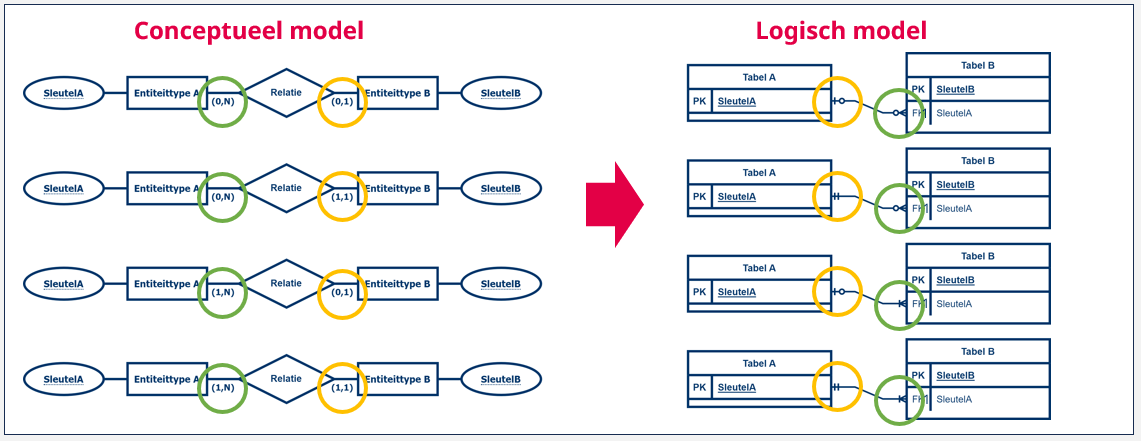
Voor elk van de 1-1 relaties doen we iets gelijkaardigs, alleen kunnen we hier kiezen vanuit welke zijde we de primaire sleutel nemen om aan de andere zijde als vreemde sleutel toe te voegen.
De richtlijn bij dit type van relatie is om naar de minimumkardinaliteit te kijken. Indien een bepaald entiteittype niet kan bestaan zonder de relatie (minimumkardinaliteit is dus ‘1‘), neemt deze tabel best de primaire sleutel van de andere tabel op als vreemde sleutel. Aangezien een entiteit enkel kan bestaan indien deze een relatie heeft, zal de rij die de entiteit beschrijft dus altijd deze waarde ingevuld moeten hebben. Want zonder deze waarde, bestaat de relatie niet.
Indien beide entiteitstypes niet zonder elkaar kunnen bestaan (beide hebben dus een minimumkardinaliteit van ‘1’), of beide allebei zonder elkaar kunnen bestaan (beide hebben dus een minimumkardinaliteit van ‘0’), mag je kiezen. Typisch kies je dan voor de tabel met het kleinste aantal rijen, om de primaire sleutel van de andere tabel op te nemen als vreemde sleutel.
Meerwaardige attributen
Meerwaardige attributen zijn een soort van 1-N relaties waarbij een entiteit gerelateerd wordt aan meerdere attribuutwaarden . Daarom moet je hiervoor een gelijkaardige aanpak toepassen als bij de omzetting van de 1-N relaties. Voor elk meerwaardig attribuut maak je een nieuwe tabel met als naam de naam van het meerwaardig attribuut. Aan deze tabel voeg je de waarde van het attribuut toe en dan vervolgens de primaire sleutel van de tabel van het entiteittype als vreemde sleutel. Vergeet dat niet om een primaire sleutel aan te duiden en een lijn in kraaienpootnotatie toe te voegen.
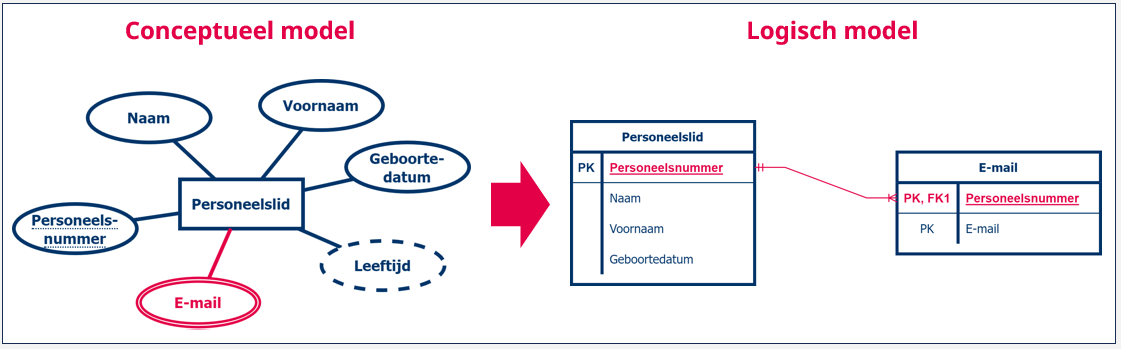
Bijvoorbeeld, het meerwaardig attribuut ‘E-mail’ van het entiteittype ‘Personeelslid’ resulteert in een tabel ‘E-mail’ met hierin een kolom ‘E-mail’. Om elk e-mailadres te kunnen verbinden aan een personeelslid, voegen we de primaire sleutel van de tabel ‘Personeelslid’ toe als vreemde sleutel aan de tabel ‘E-mail’. Merk in dit voorbeeld op dat de primaire sleutel van de tabel ‘E-Mail’ hier een samengestelde sleutel is: enkel de combinatie van de kolommen ‘Personeelsnummer’ en ‘E-mail’ is uniek.
Stap 4: voor elke N-M relatie creëren we een tussentabel
Nu wordt het even complexer.
In het voorgaande vonden we alvast een oplossing voor de verschillende entiteittypes, hun attributen en voor de 1-1 en 1-N relaties. In deze stap leggen we de focus op de N-M relaties. Om N-M relaties mogelijk te maken, moeten we verder gaan dan het eenvoudig uitwisselen van primaire sleutels omdat dit voor N-M relaties geen goede oplossing oplevert.
Laten we even starten vanuit een voorbeeld. We hebben het entiteittype ‘Student’ en het entiteittype ‘Opleidingsonderdeel’. Tussen beide entiteittypes hebben we een relatie die uitdrukt dat een student in meerdere opleidingsonderdelen kan inschrijven, en omgekeerd dat in een opleidingsonderdeel meerdere studenten kunnen inschrijven. Dat is dus een veel-op-veel relatie.
In eerste instantie maken we van beide entiteittypes twee tabellen: de tabel ‘Student’ en de tabel ‘Opleidingsonderdeel’. De eerste tabel krijgt als primaire sleutel ‘Studentennummer’, de twee tabel krijgt als primaire sleutel ‘OPOcode’. Indien we de ‘OPOcode’ zouden toevoegen aan de tabel ‘Student’, zou een student maar naar één opleidingsonderdeel kunnen verwijzen en dus maar één opleidingsonderdeel kunnen volgen, wat niet correct is. Omgekeerd, mochten we het ‘Studentennummer’ toevoegen aan de tabel ‘Opleidingsonderdeel’, zou een opleiding maar door één student kunnen worden opgenomen, wat ook niet correct is.
We lossen dit op door een tussentabel aan te maken, waaraan we voor elke combinatie waarbij een entiteit van ‘Student’ een entiteit van ‘Opleidingsonderdeel’ volgt, een rij toevoegen. Elke rij bevat dan de primaire sleutel van de tabel ‘Student’ en de primaire sleutel van de tabel ‘Opleidingsonderdeel’. De tabel zal dus twee vreemde sleutels bevatten. De combinatie van de twee vreemde sleutels, wordt dan de nieuwe primaire sleutel van de nieuwe tussentabel.
Dezelfde regels die we eerder gaven voor een sleutel, gelden hier ook. Dus indien tussen twee entiteiten meerdere relaties zijn, zou de combinatie van de vreemde sleutels mogelijk onvoldoende zijn om aan alle regels te voldoen. Dat betekent dat er mogelijk iets ontbreekt in je datamodel.
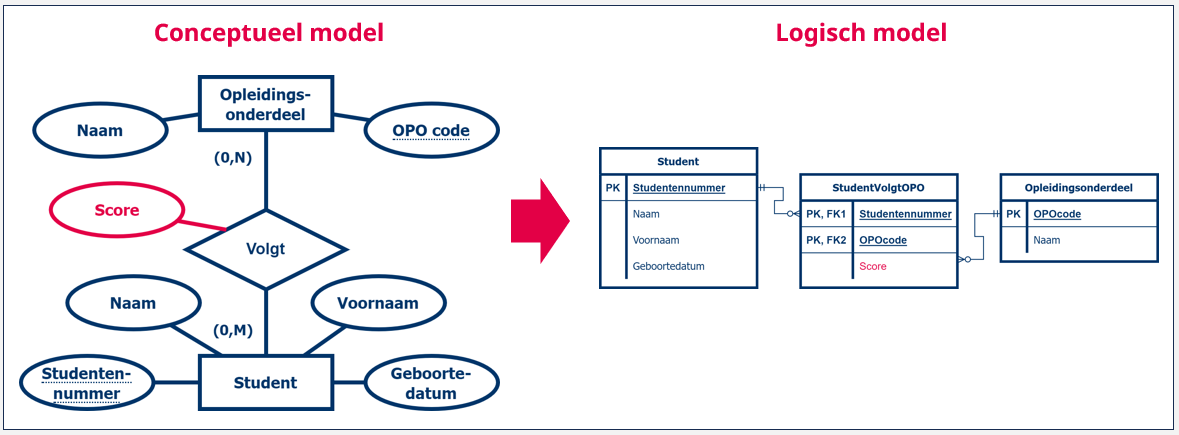
Bovenstaand voorbeeld resulteert met andere woorden in een (tussen)tabel ‘StudentVolgtOPO’ (of ‘Student_OPO’, wees consistent in je naamgeving) waarin we de kolom ‘Studentennummer’ en de kolom ‘OPOcode’ terugvinden. Beiden zijn vreemde sleutels, dus we duiden deze aan met de afkorting ‘FK’ (Foreign Key) gevolg door een volgnummer. De combinatie van beide sleutels is ook de primaire sleutel van de nieuwe tabel, dus we duiden elke kolom ook aan met afkorting ‘PK’ (Primary key). Bestudeer onderstaande figuur goed!
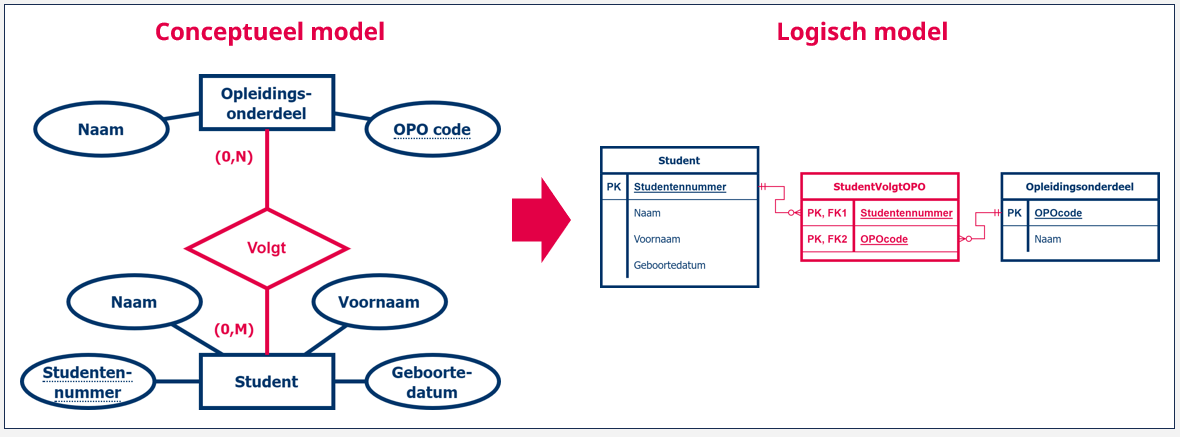
Een N-M relatie is het enige type relatie dat zelf ook attributen kan hebben. In een logisch datamodel gaan we voor deze attributen van een relatie bijkomende kolommen creëren in de tussentabel . Als we in het bovenstaand voorbeeld voor elke combinatie tussen student en opleidingsonderdeel ook een score willen bijhouden dan creëren we een bijkomende kolom ‘Score’ in de tabel ‘StudentVolgtOPO’ (zie onderstaande figuur).
Stap 5: de speciale gevallen
Er resten nog enkele constructies in het conceptueel datamodel waar we nog geen oplossing voor hebben gegeven. We willen ze toch kort even toelichten zodat jullie ook deze kunnen omzetten vanuit een conceptueel naar een logisch datamodel.
Relaties van graad 1
Een relatie van graad 1 in een conceptueel datamodel, ook wel een unaire relatie genoemd, is een situatie waarbij een entiteittype een relatie heeft met zichzelf.
Bekijk bijvoorbeeld een situatie waarbij een werknemer een andere werknemer coacht. We willen deze informatie opnemen in onze databank (en dus ook in ons datamodel). We hebben dan een entiteittype ‘Werknemer’ dat via een relatie ‘Coacht’ naar zichzelf verwijst. De relatie zegt dan vervolgens dat elke werknemer mogelijk meerdere andere werknemers coacht, maar mogelijk ook geen enkele. Daarnaast heeft elke werknemer maximaal 1 coach, maar ook dit is niet verplicht.
Om dit vervolgens om te zetten naar een logisch datamodel, behandelen we deze unaire relatie alsof het een binaire relatie is, wat overeenkomt met een 1-N relatie .
Hoe pakken we dit praktisch aan? In eerste instantie maken we een tabel ‘Werknemer’ aan en bepalen we een primaire sleutel, in dit geval ‘Personeelsnummer’. In de situatie van een 1-N relatie, dragen we de primaire sleutel van de 1-zijde (coachende werknemer) over als vreemde sleutel naar de N-zijde (gecoachte werknemer). We voegen de primaire sleutel ‘Personeelsnummer’ toe als een bijkomende kolom aan de tabel ‘Werknemer’ waarbij we die een andere naam geven, ‘PersoneelsnummerCoach‘ en we duiden die aan als vreemde sleutel met de afkorting ‘FK’, eventueel gevolgd door een volgnummer. Dit stelt ons in staat om voor elke werknemer te verbinden met zijn of haar coach omdat elke rij die de werknemer beschrijft een verwijzing bevat.
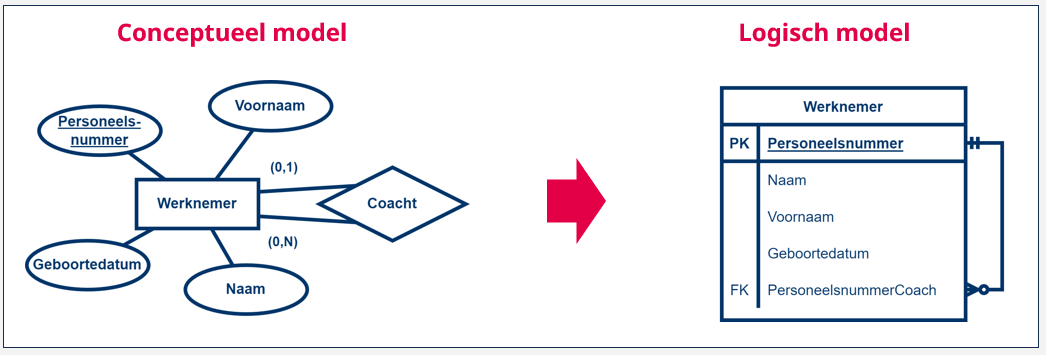
Voor de andere type relaties, loopt de redenering gelijklopend. Als een unaire relatie een N-M relatie is, maken we gebruik van een tussentabel zoals eerder beschreven werd.
Relaties van graad 3 en hoger
Een relatie van graad 3 en hoger in een conceptueel datamodel is een situatie waarbij een relatie drie of meer entiteittypes met elkaar verbindt.
Stel bijvoorbeeld een situatie voor waarbij een dokter aan een patiënt medicatie voorschrijft. Indien we dit modelleren in een conceptueel datamodel zouden we drie entiteittypes hebben ‘Dokter’, ‘Patiënt’ en ‘Medicatie’ die met elkaar verbonden zijn door een relatie ‘Schrijft voor’. We hebben dit voorbeeld eerder al gebruikt bij het conceptueel datamodel, dus we weten dat we dit niet kunnen herleiden naar binaire relaties.
Om dit vervolgens om te zetten naar een logisch datamodel, creëren we voor elk van de drie entiteittypes een tabel: ‘Dokter’, ‘Patiënt’ en ‘Medicatie’. Deze drie tabellen hebben elk een primaire sleutel, respectievelijk ‘Dokternummer’, ‘Patiëntennummer’ en ‘Medicatiecode’. De relatie vervangen we door een tussentabel ‘Voorschrift’, waaraan we drie kolommen toevoegen die elk verwijzen naar de primaire sleutels van de tabellen ‘Dokter’, ‘Patiënt’ en ‘Medicatie’. Elke code vormt een vreemde sleutel in de tabel ‘Voorschrift’ en duiden we dus aan met de afkorting ‘FK’ gevolgd door een volgnummer. De drie kolommen samen vormen de primaire sleutel van de tabel ‘Voorschrift’ en duiden we dus ook aan met de afkorting ‘PK’. Voor elke relatie die er bestaat tussen de verschillende entiteiten van de entiteittypes ‘Dokter’, ‘Patiënt’ en ‘Medicatie’ voegen we een rij toe aan de tabel ‘Voorschrift’.
Elk attribuut van de relatie, bijvoorbeeld het attribuut ‘Datum’ om aan te geven wanneer de medicatie werd voorgeschreven, wordt aan de tussentabel ‘Voorschrift’ toegevoegd als een bijkomende kolom.
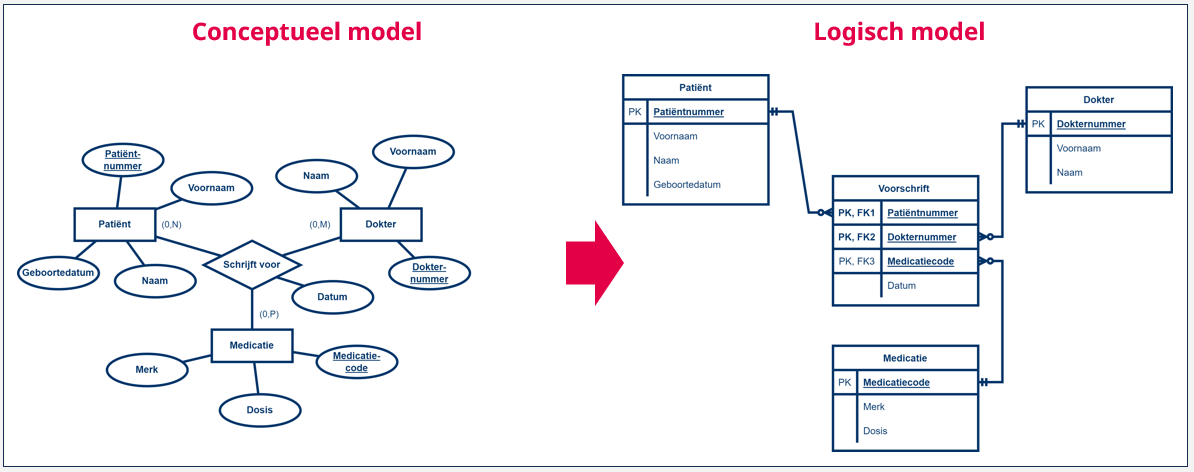
We kunnen hetzelfde principe uitbreiden voor relaties van graad 4, 5, ... Telkens creëren we een tussentabel die de primaire sleutels bevat van de andere betrokken tabellen.
Oefening autoverhuur
Maak Oefening 1: autoverhuur.
Oefening jeugdvereniging
Maak Oefening 2: jeugdvereniging.
Oefening bordspellenvereniging
Maak Oefening 3: bordspellenvereniging.
Oefening technisch onderhoud en reparatie
Maak Oefening 4: technisch onderhoud en reparatie.
Subtypes en supertypes
We hebben eerder beschreven hoe het ERD uitgebreid werd tot het EERD, waaronder de mogelijkheid om subtypes en supertypes te creëren. Een subtype is een entiteitstype dat attributen en relaties overerft van een supertype en die vervolgens uitbreidt met bijkomende attributen en relaties. Zo zagen we ook dat een supertype vervolgens meerdere subtypes kan hebben, elk een specialisatie van het supertype.
Het voorbeeld dat we eerder gebruikt hebben, was een supertype ‘Werknemer’, en twee subtypes ‘Tijdelijke werknemer’ en ‘Permanente werknemer’. Van het entiteittype ‘Werknemer’ houden we de typische eigenschappen bij: naam, voornaam, geboortedatum, werknemersnummer, ... Daarnaast hebben we het entiteittype ‘Tijdelijke werknemer’ dat alle attributen en relaties overerft van het entiteittype ‘Werknemer’, maar dit uitbreidt met de attributen ‘Startdatum contract’ en ‘Einddatum contract’. Het entiteittype ‘Permanente werknemer’ breidt het entiteittype ‘Werknemer’ uit met de attributen ‘Startdatum werknemer’ en ‘Aantal jaren dienst’.
Om dit vervolgens om te zetten naar een logisch datamodel, kunnen we verschillende strategieën toepassen. De afweging tussen de verschillende strategieën gebeurt typisch op basis van performantie, en aangezien we in dit vak nog niet echt de focus leggen op performantie, worden jullie ook niet beoordeeld op jullie keuze. Maar jullie moeten wel in staat zijn om beide strategieën toe te passen.
We overlopen de twee strategieën:
-
Een eerste strategie bestaat erin om één tabel te creëren ‘Werknemer’, waar we voor elk attribuut van het entiteittype ‘Werknemer’, met uitzondering van de meerwaardige en afgeleide attributen, een kolom toevoegen. We geven deze tabel een primaire sleutel, bijvoorbeeld ‘Personeelsnummer’. Vervolgens gaan we voor elk van de attributen van de subtypes van het entiteittype ‘Werknemer’, met andere woorden de entiteittypes ‘Tijdelijke werknemer’ en ‘Permanente werknemer’, ook kolommen toevoegen. Dit resulteert in één grote tabel met alle attributen van zowel het supertype als de subtypes. Indien de subtypes ook nog relaties hebben, moeten elk van de relaties natuurlijk ook correct verwerkt worden zoals we eerder omschreven hebben. De resulterende tabel bevat één rij voor elke werknemer, de verschillende kolommen worden ingevuld naargelang de werknemer een tijdelijk of permanent werknemer is.
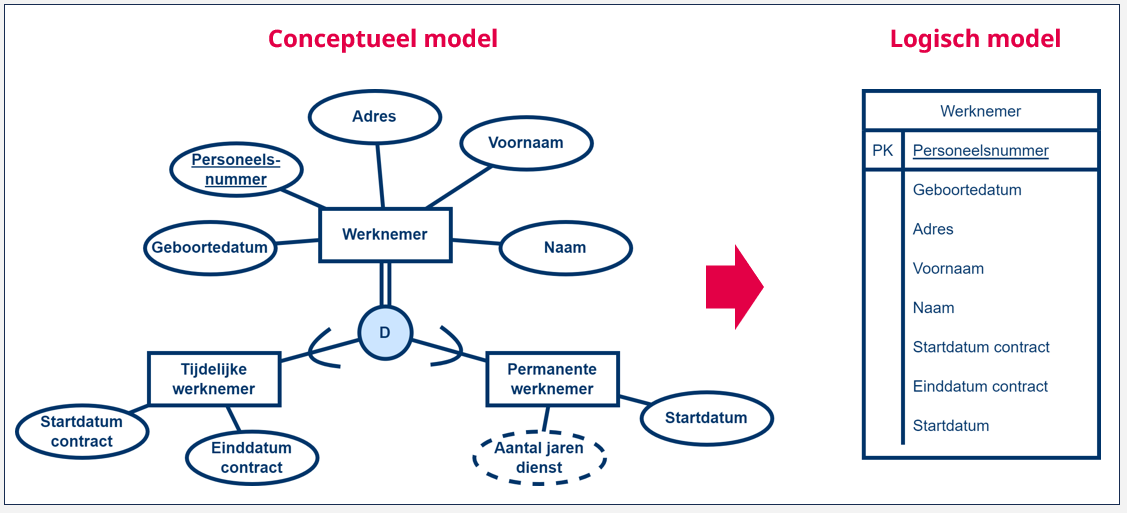
Deze strategie werkt zeer goed indien het supertype het grootste aandeel aan attributen en relaties omvat (en de hieruit volgende kolommen), en de subtypes elk slechts enkele bijkomende attributen of relaties hebben. We kiezen dus bewust om geen complexiteit te creëren door bijkomende tabellen bij te maken.
Bijkomend werkt deze strategie goed indien het gaat om overlappende en/of totale overerving . Bij overlappende en/of totale overerving gaan we telkens meer attributen ingevuld hebben van een bepaalde entiteit, of vertaald naar het logisch model zullen er voor een bepaalde rij minder kolommen leeg zijn.
-
Een tweede strategie bestaat erin om één tabel te creëren ‘Werknemer’, waar we voor elk attribuut van het entiteittype ‘Werknemer’, met uitzondering van de meerwaardige en afgeleide attributen, een kolom toevoegen. We geven deze tabel een primaire sleutel, bijvoorbeeld ‘Personeelsnummer’. Vervolgens creëren we voor elk van de subtypes bijkomende tabellen , wat voor ons voorbeeld resulteert in de tabellen ‘Tijdelijke werknemer’ en ‘Permanent werknemer’.
Ook aan deze tabellen voegen we voor elk attribuut van de subtypes, opnieuw met uitzondering van de meerwaardige en afgeleide attributen, een kolom toe. Aan elk van de subtype-tabellen voegen we de primaire sleutel van de supertype-tabel toe. In ons voorbeeld voegen we de kolom ‘Personeelsnummer’ toe aan de tabellen ‘Tijdelijke werknemer’ en ‘Permanente werknemer’. Gezien het gaat om de primaire sleutel van een andere tabel, duiden we de vreemde sleutel aan met de afkorting ‘FK’ gevolgd door een volgnummer. Tegelijk gaat deze sleutel ook de rol van primaire sleutel vervullen voor de subtype-tabellen, dus duiden we deze ook aan met de afkorting ‘PK’.
Dit resulteert in verschillende tabellen, één voor het supertype en één voor elk van de subtypes. Natuurlijk moeten ook hier de verschillende relaties correct verwerkt worden zoals we eerder omschreven hebben. De resulterende supertype-tabel bevat één rij voor elke werknemer. Bijkomend zal er voor elke tijdelijke werknemer nog een rij toegevoegd worden aan de tabel ‘Tijdelijke werknemer’ en voor elke permanente werknemer een rij aan de tabel ‘Permanente werknemer’ waarbij telkens de kolommen naargelang worden ingevuld.
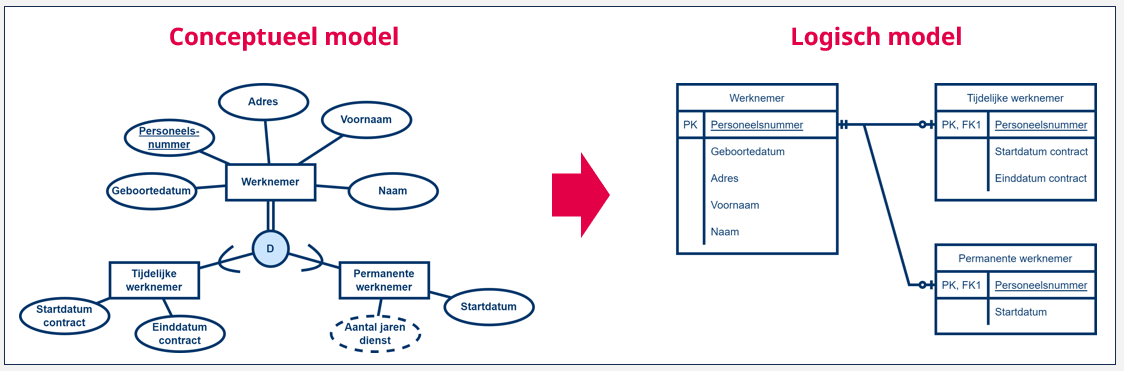
Deze strategie werkt zeer goed indien het supertype een klein aantal attributen en relaties omvat (en de hieruit volgende kolommen), en de subtypes zelf heel wat attributen of relaties hebben. Om de complexiteit van al die bijkomende kolommen die meestal leeg zouden zijn, te vermijden. Splitsen we het geheel dus op.
Bijkomend werkt deze strategie goed indien het gaat om disjuncte en/of optionele overerving . Bij zowel disjuncte en/of optionele overerving hebben we een groot risico op heel wat lege kolommen voor een bepaalde rij, wat dan weer onnodige ruimte inneemt.
Tenslotte kan je bovenstaande strategieën gaan combineren, waarbij je voor bepaalde subtypes een bijkomende tabel creëert, en andere subtypes mee opneemt in de super-type tabel.
Oefening bibliotheek
Maak Oefening 5: bibliotheek.
Redundantie in een relationeel databankmodel
In het vorige hoofdstuk hebben we kort het concept van redundantie aangehaald . Redundantie betekent dat we meerdere keren dezelfde informatie gaan bijhouden in ons datamodel. Voor het conceptueel datamodel betekent dit dat we bij het definiëren van entiteittypes, attributen en relaties erop moeten letten dat we geen logica toevoegen die al in het datamodel vervat zit.
In de context van een relationeel databankmodel, betekent redundantie dat we tabellen en kolommen gaan creëren die we eigenlijk niet nodig hebben. Maar hoe loopt dit dan?
Laten we starten vanuit het voorbeeld dat we eerder gebruikten. Een klant koopt een wagen in één van de garages. We weten welke klant welke wagen koopt. We weten ook in welke garage een wagen verkocht wordt. Indien we willen weten in welke garage een klant een wagen koopt, kunnen we de relatie ‘Koopt wagen in’ tussen de entiteittypes ‘Klant’ en ‘Garage‘ toevoegen. We hebben eerder gezegd dat deze relatie redundant is, omdat de informatie die we uit deze relatie kunnen afleiden, ook al vervat zit in de relatie ‘Koopt’ tussen de entiteittypes ‘Klant’ en ‘Wagen’ en de relatie ‘Staat in’ tussen de entiteittypes ‘Wagen’ en ‘Garage’. Wat zou het nu betekenen voor ons logisch datamodel als we de relatie toch toevoegen?
Op basis van het bovenstaande, komen we mogelijk tot het onderstaande conceptueel datamodel. We hebben kardinaliteiten en bijkomende attributen toegevoegd.
Als we dit datamodel nu vertalen naar een logisch datamodel, krijgen we het onderstaande resultaat.
Er is nu redundantie. Want als we willen weten welke klant een wagen heeft gekocht in een bepaalde garage, kunnen we kijken naar de tabel ‘Koopt_wagen_in’. We kunnen ook kijken in de tabel ‘Wagen’, want voor elke verkochte wagen staat er in deze tabel een verwijzing naar zowel de klant als de garage. Maar waarom is dit een probleem?
Wanneer we binnen een model via verschillende wegen dezelfde informatie voorstellen, is er een risico dat er anomalieën ontstaan binnen de databank . De mogelijke types van anomalieën zijn:
- Insert anomalieën
- Delete anomalieën
- Update anomalieën
Kort gezegd kan het zijn dat we in de tabel ‘Wagen’ data toevoegen (insert), data verwijderen (delete) of data aanpassen (update) zonder dat diezelfde data aangepast wordt in de tabel ‘Koopt_wagen_in’ en omgekeerd. Dit is een probleem omdat we zo de integriteit van onze databank in gevaar brengen.
Met integriteit van een databank bedoelen we dat de data in de databank de werkelijkheid correct weerspiegelt. Als bijvoorbeeld een verkoop niet doorgaat, gaan we in de tabel ‘Wagen’ de verwijzing naar een klant verwijderen. Mochten we de verwijzing naar deze verkoop in de tabel ‘Koopt_wagen_in’ vergeten te verwijderen, dan is de data in de databank niet meer correct. In de tabel ‘Koopt_wagen_in’ hebben we een verkoop geregistreerd, maar in de tabel ‘Wagen’ niet. Dit is een voorbeeld van een update anomalie.
Redundantie is in principe niet altijd slecht, maar zoals boven beschreven kan het wel voor een verhoogd risico op problemen zorgen. Daarom zullen we dit proberen te vermijden waar mogelijk. Toch zijn er bepaalde databankmodellen waarbij redundantie geen probleem vormt, voor dit type databanken zorgt redundantie net voor een verhoogde performantie. Dit is echter niet het type databank dat we in dit vak zullen behandelen.
Voor relationele datamodellen zijn er een aantal standaarden geformuleerd die redundantie trachten te vermijden. Deze standaarden worden normaalvormen genoemd. We gaan deze kort toelichten zodat jullie weten wat het normaliseren van een datamodel inhoudt.
Normaliseren
Om redundantie in een datamodel te vermijden, gaan we het datamodel normaliseren. Normalisatie is het proces waarbij we een datamodel (en de uiteindelijke databank) gaan structureren in logische eenheden. Om ons hierin te begeleiden maken we gebruik van normaalvormen, waarbij elke normaalvorm bepaalde voorwaarden oplegt aan de tabellen in het datamodel. De voorwaarden die vervat zitten in deze normaalvormen hebben als doel redundantie te beperken en integriteit te garanderen.
De theoretische achtergrond van normaalvormen is gebaseerd op eerste-orde logica waarbij de afhankelijkheden die bestaan tussen de verschillende kolommen, waarbij bijvoorbeeld de kolom ‘Postcode’ de kolom ‘Gemeente‘ bepaalt, worden weggewerkt om redundantie van data weg te werken.
We geven hieronder een idee van de eerste drie normaalvormen. Er zijn in totaal zes normaalvormen, maar in deze vereenvoudigde kennismaking gaan we op die laatste drie normaalvormen niet in.
Eerste normaalvorm
De eerste normaalvorm, 1NF (‘first normal form’), zegt dat een tabel in 1NF is indien geen enkele waarde in de tabel zelf een tabel is. Met andere woorden, als een entiteittype een meerwaardig attribuut heeft, moeten we voor dit attribuut bij de omzetting van het conceptueel datamodel naar een logisch datamodel, een aparte tabel creëren, net zoals we hierboven hebben beschreven. Van elke tabel die voldoet aan deze voorwaarde, kunnen we zeggen dat deze in eerste normaalvorm is.
Tweede normaalvorm
De tweede normaalvorm, 2NF (‘second normal form’), zegt dat een tabel voldoet aan:
- de eerste normaalvorm,
- en dat elke kolom van de tabel (die geen onderdeel is van een kandidaatsleutel voor de tabel) telkens afhankelijk is van het geheel van de tabellen die onderdeel vormen van een kandidaatsleutel.
De tweede voorwaarde is wat complex. Eerst en vooral hebben we het begrip ‘afhankelijk’, wat eigenlijk betekent dat de waarde van een kolom de waarde van een andere kolom bepaalt. Bijvoorbeeld, we hebben een tabel ‘Adres’ die adressen bevat. De tabel bevat de kolommen ‘Straat’, ‘Huisnr’, ‘Postcode’ en ‘Gemeente’. De enige kandidaatsleutel is een combinatie van ‘Straat’, ‘Huisnr’ en ‘Postcode’. Als we de waarde weten voor elk van deze drie kolommen, kunnen we de juiste rij bepalen.
De kolom ‘Gemeente’ is afhankelijk van de kolom ‘Postcode’, want als we de waarde van ‘Postcode’ kennen, kunnen we de waarde van ‘Gemeente’ bepalen. Zo is 3053 de postcode van Oud-Heverlee (deelgemeente Haasrode). Omgekeerd is de kolom ‘Postcode’ niet afhankelijk van de kolom ‘Gemeente’, want als we de waarde van ‘Gemeente’ kennen, kunnen we de waarde van ‘Postcode’ niet eenduidig bepalen. Zo heeft de gemeente Oud-Heverlee de postcodes 3053 (Oud-Heverlee), 3051 (Sint-Joris-Weert), 3052 (Blanden), 3053 (Haasrode) en 3053 (Vaalbeek). Al deze deelgemeenten zijn ‘Oud-Heverlee’. De postcode bepaalt dus uniek de gemeente, maar de gemeente bepaalt niet uniek de postcode. De kolom ‘Gemeente’ is dus afhankelijk van de kolom ‘Postcode’, maar de kolom ‘Postcode’ is niet afhankelijk van de kolom ‘Gemeente'.
‘Postcode’ is onderdeel van een kandidaatsleutel, maar is op zich geen kandidaatsleutel. De kolom ‘Gemeente’ is niet afhankelijk van het geheel van de tabellen die onderdeel vormen van een kandidaatsleutel, maar slechts van één tabel van een kandidaatsleutel. De tweede voorwaarde wordt dus niet ingevuld.
| Straat | Huisnr | Postcode | Gemeente |
|---|---|---|---|
| Stationlei | 12 | 1800 | Vilvoorde |
| Bondgenotenlaan | 16 | 3000 | Leuven |
| Maurice Dequeeckerplein | 1 | 2100 | Deurne |
| Maurice Dequeeckerplein | 26 | 2100 | Deurne |
| Turnhoutsebaan | 20 | 2100 | Deurne |
| Molenberg | 14 | 3290 | Deurne |
Om aan de tweede voorwaarde te voldoen, moeten we deze kolom opdelen in twee aparte tabellen. Een eerste tabel ‘Adres’ bestaat uit de kolommen ‘Straat’, ‘Huisnr’ en ‘Postcode'.
| Straat | Huisnr | Postcode |
|---|---|---|
| Stationlei | 12 | 1800 |
| Bondgenotenlaan | 16 | 3000 |
| Maurice Dequeeckerplein | 1 | 2100 |
| Maurice Dequeeckerplein | 26 | 2100 |
| Turnhoutsebaan | 20 | 2100 |
| Molenberg | 14 | 3290 |
Vervolgens maken we een twee tabel ‘Gemeente’ die de kolommen ‘Postcode' en ‘Gemeente’ bevatten.
| Postcode | Gemeente |
|---|---|
| 1800 | Vilvoorde |
| 3000 | Leuven |
| 2100 | Deurne |
| 3290 | Deurne |
Onze tabellen voldoen nu allebei aan de tweede voorwaarde van 2NF.
Derde normaalvorm
De derde normaalvorm, 3NF van third normal form, zegt dat een tabel voldoet aan:
- de tweede normaalvorm,
- dat elke kolom van de tabel telkens enkel afhankelijk is van één van de kandidaatsleutels.
De tweede normaalvorm stelt dat alle kolommen die niet tot een kandidaatsleutel behoren, afhankelijk moeten zijn van de volledige kandidaatsleutels en dus niet afhankelijk mogen zijn van slechts een stukje van een kandidaatsleutel.
De derde normaalvorm breidt dit uit zodat alle kolommen die niet tot een kandidaatsleutel behoren, enkel afhankelijk mogen zijn van de kandidaatsleutel. Indien een kolom die niet tot een kandidaatsleutel behoort, afhankelijk is van een andere kolom dan de kandidaatsleutel, verwijderen we deze afhankelijkheid door de tabel te splitsen.
Bijvoorbeeld, we hebben een tabel ‘Personeelslid’ die gegevens van personeelsleden bevat. De tabel bevat de kolommen ‘Personeelsnummer’, ‘Naam’, ‘Straat’, ‘Huisnr’, ‘Postcode’ en ‘Gemeente'. De enige kandidaatsleutel is ‘Personeelsnummer'. Elke waarde is enkelvoudig, dus we voldoen aan 1NF. Elk van de waardes van de andere kolommen wordt bepaald door de waarde van ‘Personeelsnummer’, dus we voldoen aan 2NF. Opnieuw wordt de kolom ‘Gemeente’ bepaald door de kolom ‘Postcode'. ‘Postcode’ is hier geen onderdeel van een kandidaatsleutel. Er bestaat dus een kolom die NIET enkel afhankelijk is van één van de kandidaatsleutels, dus we voldoen niet aan de tweede voorwaarde van 3NF.
| Personeelsnr | Naam | Straat | Huisnr | Postcode | Gemeente |
|---|---|---|---|---|---|
| 0000001 | Jan | Stationlei | 12 | 1800 | Vilvoorde |
| 0000002 | Kaat | Bondgenotenlaan | 16 | 3000 | Leuven |
| 0000003 | Hans | Maurice Dequeeckerplein | 1 | 2100 | Deurne |
| 0000004 | Petra | Maurice Dequeeckerplein | 26 | 2100 | Deurne |
| 0000005 | Kaat | Turnhoutsebaan | 20 | 2100 | Deurne |
| 0000006 | Pieter | Molenberg | 14 | 3290 | Deurne |
Om aan de tweede voorwaarde te voldoen, moeten we deze kolom opdelen in twee aparte tabellen. Een eerste tabel ‘Adres’ bestaat uit de kolommen ‘Straat’, ‘Huisnr’ en ‘Postcode'. Vervolgens maken we een twee tabel ‘Gemeente’ die de kolommen ‘Postcode’ en ‘Gemeente’ bevatten.
| Personeelsnummer | Naam | Straat | Huisnr | Postcode |
|---|---|---|---|---|
| 0000001 | Jan | Stationlei | 12 | 1800 |
| 0000002 | Kaat | Bondgenotenlaan | 16 | 3000 |
| 0000003 | Hans | Maurice Dequeeckerplein | 1 | 2100 |
| 0000004 | Petra | Maurice Dequeeckerplein | 26 | 2100 |
| 0000005 | Kaat | Turnhoutsebaan | 20 | 2100 |
| 0000006 | Pieter | Molenberg | 14 | 3290 |
| Postcode | Gemeente |
|---|---|
| 1800 | Vilvoorde |
| 3000 | Leuven |
| 2100 | Deurne |
| 3290 | Deurne |
Onze tabellen voldoen nu allebei aan de tweede voorwaarde van 3NF.
Conclusies
Het normaliseren heeft een impact op je logisch datamodel. Van zodra je beslist om een tabel op te splitsen, pas je dit ook aan in je logisch model. Dit betekent dat je ook de relaties moet aanpassen of toevoegen.
We verwachten niet dat jullie een model in een bepaalde normaalvorm kunnen omzetten. Wel verwachten we dat jullie het concept normaliseren kunnen uitleggen, en dat jullie bewust omgaan met het creëren van redundantie.